Quick Reference for Fairness Measures

Fairness Metrics

Metrics by Category

There are three common categories of metrics for determining whether a model is considered “fair”: Group Fairness, which compares the statistical similarities of predictions relative to known and discrete protected groupings; Similarity-Based Measures, which evaluate predictions without those discrete protected groups; and Causal Reasoning measures, which evaluate fairness through the use of causal models.

Category	Metric	Definition	Weakness	References
Group Fairness	Demographic Parity	A model has Demographic Parity if the predicted positive rates (selection rates) are approximately the same for all protected attribute groups: $\dfrac{P(\hat{y}=1\lvert unprivileged)}{P(\hat{y}=1\rvert privileged)}$ Harms Addressed: Allocative	Historical biases present in the data are not addressed and may still bias the model.	Zafar et al (2017)
	Equalized Odds	Odds are equalized if P(+) is approximately the same for all protected attribute groups. Equal Opportunity is a special case of equalized odds specifying that P(+ \| y = 1) is approximately the same across groups. Harms Addressed: Allocative, Representational	Historical biases present in the data are not addressed and may still bias the model.	Hardt et al (2016)
	Predictive Parity	This parity exists where the Positive Predictive Value is approximately the same for all protected attribute groups. Harms Addressed: Allocative, Representational	Historical biases present in the data are not addressed and may still bias the model.	Zafar et al (2017)

Similarity-Based Measures	Individual Fairness	Individual fairness exists if “similar” individuals (ignoring the protected attribute) are likely to have similar predictions. Harms Addressed: Representational	The appropriate metric for similarity may be ambiguous.	Dwork (2012), Zemel (2013), Kim et al (2018)
	Entropy-Based Indices	Measures of entropy, particularly existing inequality indices from the field of economics, are applied to evaluate either individuals or groups Harms Addressed: Representational		Speicher (2018)
	Unawareness	A model is unaware if the protected attribute is not used. Harms Addressed: Allocative, Representational	Removal of a protected attribute may be ineffectual due to the presence of proxy features highly correlated with the protected attribute.	Zemel et al (2013), Barocas and Selbst (2016)

Causal Reasoning	Counterfactual Fairness *	Counterfactual fairness exists where counterfactual replacement of the protected attribute does not significantly alter predictive performance. This counterfactual change must be propogated to correlated variables. Harms Addressed: Allocative, Representational	It may be intractable to develop a counterfactual model.	Russell et al (2017)

Statistical Definitions of Group Fairness

Metric	Criteria	Definition	Description
Demographic Parity	Statistical Independence	$R{\perp}G$	Sensitive attributes (A) are statistically independent of the prediction result (R)
Equalized Odds	Statistical Separation	$R{\perp}A\rvert{Y}$	Sensitive attributes (A) are statistically independent of the prediction result (R) given the ground truth (Y)
Predictive Parity	Statistical Sufficiency	$Y{\perp}A\rvert{R}$	Sensitive attributes (A) are statistically independent of the ground truth (Y) given the prediction (R)

From: Verma & Rubin, 2018

Fairness Measures

Name	Definition	About	Aliases
Demographic Parity	$P(\hat{y}\lvert{G=u})=P(\hat{y}\lvert{G=p})$	Predictions must be statistically independent from the sensitive attributes. Subjects in all groups should have equal probability of being assigned to the positive class. Note: may fail if the distribution of the ground truth justifiably differs among groups Criteria: Statistical Independence	Statistical Parity, Equal Acceptance Rate, Benchmarking
Conditional Statistical Parity	$P(\hat{y}=1\lvert{L=l,G=u})=P(\hat{y}=1\lvert{L=l,G=p})$	Subjects in all groups should have equal probability of being assigned to the positive class conditional upon legitimate factors (L). Criteria: Statistical Separation
False positive error rate (FPR) balance	$P(\hat{y}=1\lvert{Y=0,G=u})=P(\hat{y}=1\lvert{Y=0,G=p})$	Equal probabilities for subjects in the negative class to have positive predictions. Mathematically equivalent to equal TNR: $P(d=0\lvert{Y=0,G=m})=P(d=0\lvert{Y=0,G=f})$ Criteria: Statistical Separation	Predictive Equality
False negative error rate (FNR) balance	$P(\hat{y}=0\lvert{Y=1,G=u})=P(\hat{y}=0\lvert{Y=1,G=p})$	Equal probabilities for subjects in the positive class to have negative predictions. Mathematically equivalent to equal TPR: $P(d=1\lvert{Y=1,G=m})=P(d=1\lvert{Y=1,G=f})$ Criteria: Statistical Separation	Equal Opportunity
Equalized Odds	$P(\hat{y}=1\lvert{Y=c,G=u})=P(\hat{y}=1\lvert{Y=c,G=p}),{c}\in{0,1}$	Equal TPR and equal FPR. Mathematically equivalent to the conjunction of FPR balance and FNR balance Criteria: Statistical Separation	Disparate mistreatment, Conditional procedure accuracy equality
Predictive Parity	$P(Y=1\lvert{\hat{y}=1,G=u})=P(Y=1\lvert{\hat{y}=1,G=p})$	All groups have equal PPV (probability that a subject with a positive prediction actually belongs to the positive class. Mathematically equivalent to equal False Discovery Rate (FDR): $P(Y=0\lvert{d=1,G=m})=P(Y=0\lvert{d=1,G=f})$ Criteria: Statistical Sufficiency	Outcome Test
Conditional use accuracy equality	$(P(Y=1\lvert{\hat{y}=1,G=u})=P(Y=1\lvert{\hat{y}=1,G=p}))$ $\wedge (P(Y=0\lvert{\hat{y}=0,G=u})=P(Y=0\lvert{\hat{y}=0,G=p}))$	Criteria: Statistical Sufficiency
Overall Accuracy Equity	$P(\hat{y}=Y,G=m)=P(\hat{y}=Y,G=p)$	Use when True Negatives are as desirable as True Positives
Treatment Equality	$FNu/FPu=FNp/FPp$	Groups have equal ratios of False Negative Rates to False Positive Rates
Calibration	$P(Y=1\lvert{S=s,G=u})=P(Y=1\lvert{S=s,G=p})$	For a predicted probability score S, both groups should have equal probability of belonging to the positive class Criteria: Statistical Sufficiency	Test-fairness, matching conditional frequencies
Well-calibration	$P(Y=1\lvert{S=s,G=u})=P(Y=1\lvert{S=s,G=p})=s$	For a predicted probability score S, both groups should have equal probability of belonging to the positive class, and this probability is equal to S Criteria: Statistical Sufficiency
Balance for positive class	$E(S\lvert{Y=1,G=u})=E(S\lvert{Y=1,G=p})$	Subjects in the positive class for all groups have equal average predicted probability score S Criteria: Statistical Separation
Balance for negative class	$E(S\lvert{Y=0,G=u})=E(S\lvert{Y=0,G=p})$	Subjects in the negative class for all groups have equal average predicted probability score S Criteria: Statistical Separation

Causal discrimination	$(X_p=X_u\wedge G_p!=G_u)\rightarrow\hat{y}_u=\hat{y}_p$	Same classification produced for any two subjects with the exact same attributes
Fairness through unawareness	$X_i=X_j\rightarrow\hat{y}_i=\hat{y}_j$	No sensitive attributes are explicitly used in the decision-making process Criteria: Unawareness
Fairness through awareness (Individual Fairness)	for a set of applicants V , a distance metric between applicants k : V Å~V → R, a mapping from a set of applicants to probability distributions over outcomes M : V → δA, and a distance D metric between distribution of outputs, fairness is achieved iff $D(M(x),M(y))≤k(x,y)$	Similar individuals (as defined by some distance metric) should have similar classification	Individual Fairness
Counterfactual fairness	A causal graph is counterfactually fair if the predicted outcome d in the graph does not depend on a descendant of the protected attribute G.

Interpretation of Common Measures

Group Measure Type	Examples	“Fair” Range
Statistical Ratio	Disparate Impact Ratio, Equalized Odds Ratio	0.8 <= “Fair” <= 1.2
Statistical Difference (Binary Classification)	Equalized Odds Difference, Predictive Parity Difference	-0.1 <= “Fair” <= 0.1
Statistical Difference (Regression)	MAE Difference, Mean Prediction Difference	Problem Specific

Metric	Measure	Equation	Interpretation
Group Fairness Measures - Binary Classification	Selection Rate	$\dfrac{\sum_{i=0}^N \hat{y}_i}{N}$	-
	Demographic (Statistical) Parity Difference	$P(\hat{y}=1\lvert unprivileged)-P(\hat{y}=1\rvert privileged)$	(-) favors privileged group (+) favors unprivileged group
	Disparate Impact Ratio (Demographic Parity Ratio)	$\dfrac{P(\hat{y}=1\ \rvert u)}{P(\hat{y}=1\ \rvert p)}=\dfrac{selection\_rate(\hat{y}_{u})}{selection\_rate(\hat{y}_{p})}$	< 1 favors privileged group > 1 favors unprivileged group
	Positive Rate Difference	$precision({\hat{y}}_{u})-precision({\hat{y}}{u})$	(-) favors privileged group (+) favors unprivileged group
	Average Odds Difference	$\dfrac{(FPR_{u}-FPR_{p}) (TPR_{u}-TPR_{p})}{2}$	(-) favors privileged group (+) favors unprivileged group
	Average Odds Error	$\dfrac{\left\lvert FPR_{u}-FPR_{p}\right\rvert \left\lvert TPR_{u}-TPR_{p}\right\rvert}{2}$	(-) favors privileged group (+) favors unprivileged group
	Equal Opportunity Difference	$recall({\hat{y}}_{u})-recall({\hat{y}}_{p})$	(-) favors privileged group (+) favors unprivileged group
	Equal Odds Difference	$max((FPR_{u}-FPR_{p}),(TPR_{u}-TPR_{p}))$	(-) favors privileged group (+) favors unprivileged group
	Equal Odds Ratio	$min(\dfrac{FPR_{u}}{FPR_{p}},\dfrac{TPR_{u}}{TPR_{p}})$	< 1 favors privileged group > 1 favors unprivileged group
Group Fairness Measures - Regression	Mean Prediction Ratio	$mean\_prediction\_ratio=\dfrac{\mu(\hat{y}_{u})}{\mu(\hat{y}_{p})}$	< 1 favors privileged group > 1 favors unprivileged group
	Mean Prediction Difference	$mean\_difference=\mu(\hat{y}_{u})-\mu(\hat{y}_{p})$	(-) favors privileged group (+) favors unprivileged group
	MAE Ratio	$MAE\_ratio=\dfrac{MAE_u}{MAE_p}$	< 1 favors privileged group > 1 favors unprivileged group
	MAE Difference	$MAE\_difference=MAE_u-MAE_p$	(-) favors privileged group (+) favors unprivileged group
Individual Fairness Measures	Consistency Score	$1-\frac{1}{n\cdot{N_{n_neighbors}}}*\sum_{i=1}^n\lvert\hat{y}_i-\sum_{j\in\mathcal{N}_{neighbors}(x_i)}\hat{y}_j\rvert$	1 is consistent 0 is inconsistent
	Generalized Entropy Index		-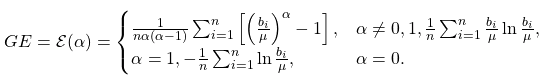
	Generalized Entropy Error	$GE(\hat{y}_i-y_i 1)$	-
	Between-Group Generalized Entropy Error	$GE([N_{u}mean(Error_{u}),N_{p}mean(Error_{p})])$	0 is fair (+) is unfair

References

Agarwal, A., Beygelzimer, A., Dudík, M., Langford, J., & Wallach, H. (2018). A reductions approach to fair classification. In International Conference on Machine Learning (pp. 60-69). PMLR. Available through arXiv preprint:1803.02453.

Barocas, S., & Selbst AD (201). Big data’s disparate impact. California Law Review, 104, 671. Retrieved from https://www.cs.yale.edu/homes/jf/BarocasDisparateImpact.pdf

Dwork, C., Hardt, M., Pitassi, T., Reingold, O., & Zemel, R. (2012, January). Fairness through awareness. In Proceedings of the 3rd innovations in theoretical computer science conference (pp. 214-226). Retrieved from https://arxiv.org/pdf/1104.3913.pdf

Hardt, M., Price, E., & Srebro, N. (2016). Equality of opportunity in supervised learning. In Advances in neural information processing systems (pp. 3315-3323). Retrieved from http://papers.nips.cc/paper/6374-equality-of-opportunity-in-supervised-learning.pdf

Kim, M., Reingol, O., & Rothblum, G. (2018). Fairness through computationally-bounded awareness. In Advances in Neural Information Processing Systems pp. 4842-4852). Retrieved from https://arxiv.org/pdf/1803.03239.pdf

Russell, C., Kusner, M.J., Loftus, J., & Silva, R. (2017). When worlds collide: integrating different counterfactual assumptions in fairness. In Advances in Neural Information Processing Systems (pp. 6414-6423). Retrieved from https://papers.nips.cc/paper/7220-when-worlds-collide-integrating-different-counterfactual-assumptions-in-fairness.pdf

Verma, S., & Rubin, J. (2018, May). Fairness definitions explained. In 2018 ieee/acm international workshop on software fairness (fairware) (pp. 1-7). IEEE.

Zemel, R., Wu, Y., Swersky, K., Pitassi, T., & Dwork, C. (2013, February). Learning fair representations. International Conference on Machine Learning (pp. 325-333). Retrieved from http://proceedings.mlr.press/v28/zemel13.pdf

Zafar, M.B., Valera, I., Gomez Rodriguez, M., & Gummadi, K.P. (2017, April). Fairness beyond disparate treatment & disparate impact: Learning classification without disparate mistreatment. In Proceedings of the 26th international conference on world wide web (pp. 1171-1180). https://arxiv.org/pdf/1610.08452.pdf